ActionData↑

経験年数が2倍だからといって経験値まで2倍になるわけではない

　仕事においても、人が経験する刺激や学びは、経験年数に反比例して少なくなります。 これは、年齢に比例して時間の流れを速く感じるようになることと同様です。 この法則はジャネの法則として知られています。 ここでは、ジャネの法則を参考に、経験年数から経験値を大雑把にモデリングし、経験年数と経験値の関係を探ります。 より正確にモデリングする場合は、経験曲線や学習曲線を利用します。

　体感時間は年齢に反比例するというのがジャネの法則です。 これを数式で表現すると以下のようになります。
　　　
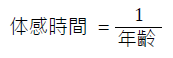
体感時間を刺激や学び、年齢を経験年数、面積を経験値と見なします。 よって、以下のように定積分し、経験年数から経験値を求めます。
　　　
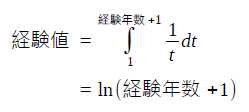
ここでは、自然対数を利用します。 この対数関数の値自体には意味がない点に注意しなければなりません。 そしてこの経験値を元に、以下のように経験年数と経験値の関係を明らかにしていきます。

　　　

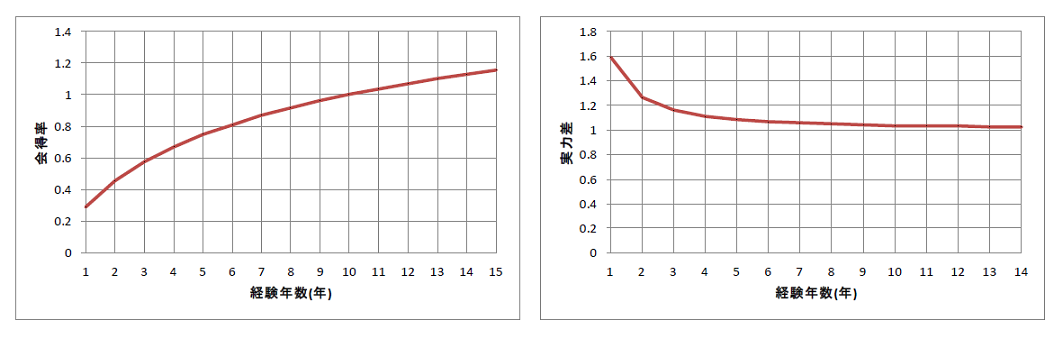
　左側のグラフは会得率であり、右側のグラフは実力差です。 それぞれ以下のように計算します。
　　　
規定年数が10年のため、会得率は10年で1になります。 一方、実力差は、経験年数が5年程度でほぼ1(差がない)となっています。 コツコツやることは大切ですが、積み重ねた経験値は意外と追い抜かれるものであることが分かります。

「協力」の名目の下に、嫌な仕事を人に押し付け合う

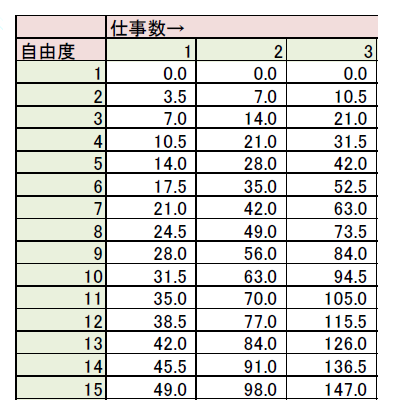
　従業員には絶えず、仕事したくない、もしくは、自分より楽している人が許せない、という思惑があります。 ゆえに仕事に対して、まずは誰かに振ることができないかと、いちいち検討するものです。 結論から言うと、目の前の仕事から逃げる従業員の(仕事の振り先という意味での)自由度は上げるべきではありません。 というのも、仕事から逃げようとすればするほど、自由度に比例して以下のように無駄が発生するためです。

　　　

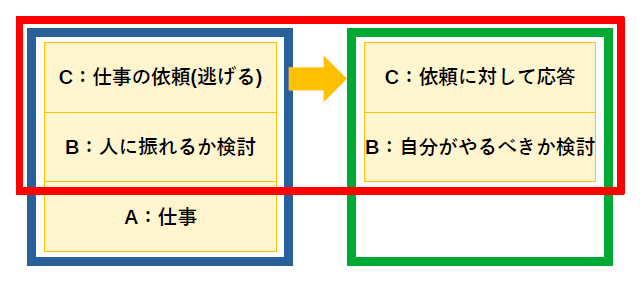
　上の図は、依頼者(青枠)と被依頼者(緑枠)の関係です。 依頼者が自分の仕事Aを人に振れるか検討Bし、推移率pで被依頼者に依頼Cした場合、被依頼者は検討Bおよび応答Cします。 この、仕事A以外の箇所(赤枠)が無駄に相当し、
　　　無駄 ＝ 仕事数 × ((B ＋ p×C ＋ p×B ＋ p×C) × (自由度－1))
と数式で表すことができます。 ここで自由度は振り先数+1です。 この式を、仕事Aを20、検討Bを1、依頼Cを2、推移率pを50%、として計算した結果が下の表です。 自由度に比例して無駄が増えていく様子が分かります。

　　　

集団になるとその規模に比例してサボる人が現れる

　組織である以上、集団で仕事します。 となると従業員は、一人くらい手を抜いても結果は変わらないだろうと考えます。 そして手抜きする人が現れます。 この割合と程度は集団の規模に比例します。 このような心理効果をリンゲルマン効果と言います。 リンゲルマン効果による生産性の低下を防ぐためには、一人一人の成果を確認し評価できる体制を構築しなければなりません。 加えて、モチベーションを低下させない工夫も必要です。

　ここで、生産性が低下する例を紹介します。 とあるサービス業の会社にて、お客様に提供する商品・サービスは、提供前に、ミスがないか2人体制で確認しています。 このとき、
　　　従業員A：確認の信頼度90%
　　　従業員B：確認の信頼度90%
の精度であることが分かっています。 よって、2人体制における信頼度は、
　　　1 － (1 － 90%) × (1 － 90%)
となり、99%となります。 これは、100回に1回ミスする確率です。 しかし実際は、
　　　従業員A：どうせこの後、従業員Bが確認するのだから、適当でいいや～
　　　従業員B：どうせ従業員Aがしっかり確認したのだから、適当でいいや～
と、お互いがお互いに甘えて、適当に確認するようになります。 このため、
　　　従業員A：確認の信頼度70%
　　　従業員B：確認の信頼度70%
と精度が低下してしまいます。 よって、2人体制における信頼度は、
　　　1 － (1 － 70%) × (1 － 70%)
となり、信頼度は91%まで落ちることになります。 これは1人で確認した場合とほぼ同程度の精度です。

　また、リンゲルマン効果はモチベーションと関係が深いものです。 モチベーションは、労力と報酬または責任に依存します。 集団化すると、労力に対する報酬または責任が制限されます。 よって生産性が低下するという効果が、リンゲルマン効果です。 集団の規模と生産性の関係では、
　　　・仕事内容
　　　・従業員の志向
　　　・従業員の熟練度
　　　・監督者または評価者
　　　・プレッシャー
　　　・成功時の報酬
　　　・失敗時の責任
など、複数の要因が複雑に絡み合っています。

人を介して人を見る、人を介して人に頼る

　自分が相手を評価できなくとも、評価できる人の評価を介することで、その相手を評価できるようになります。 もしくは、自分に相手への影響力がなくとも、影響力のある人を介することで、相手に働きかけることができるようになります。 このように人を介することで、できることの範囲が広がります。 ただし、人を介して人を評価したり、人を介して人に働きかける場合は、自分が直接そうする場合と比較して以下のような違いが表れます。 まず、人を介して人を評価する場合です。

　　　

　　　①A→Bが高評価で、B→Cが高評価 ⇒ A→Cは高評価となる
　　　②A→Bが高評価で、B→Cが低評価 ⇒ A→Cは低評価となる
　　　③A→Bが低評価で、B→Cが高評価 ⇒ A→Cは低評価となる
　　　④A→Bが低評価で、B→Cが低評価 ⇒ A→Cは低評価となる

人を介して評価する場合、低評価される人が増える傾向にあります。 つまり組織を上から見ると多くの人が無能に見えるということです。 次いで以下は、人を介して人に働きかける場合です。

　　　

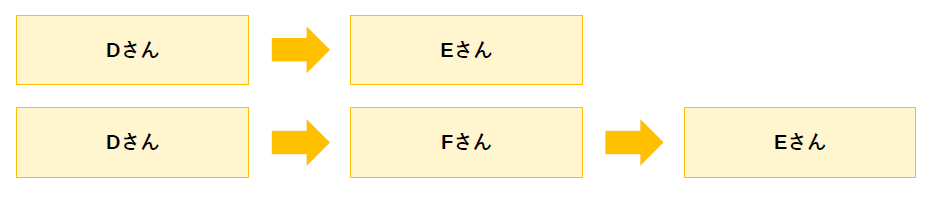
D→Eの影響力が100であれば、当然ながら、D→Eのアプローチでは100の影響力しか発揮されません。 しかしもし、F→Eの影響力が200であり、かつ、D→Fの影響力が150であれば、Fを介してD→F→Eとアプローチすることで150の影響力が発揮されます。 誰をどこに配置させる(出世させる)か決めるにあたって、こうした影響力の観点も考慮した方がいいということです。

人は自分を上回らないように調整して相手を評価する

　アキレスとカメは、アキレスと100m先のカメが競争したとき、アキレスが100m進む間にカメは10m進み、アキレスが10m進む間にカメは1m進み、アキレスが1m進む間にカメは0.1m進み、…、と繰り返し、いつまでたってもアキレスがカメを追い抜けないというパラドックスです。 同様に評価の場合も、人は自分を上回らないように相手を評価するため、自分に近づけば近づくほど小さく評価します。

　　　

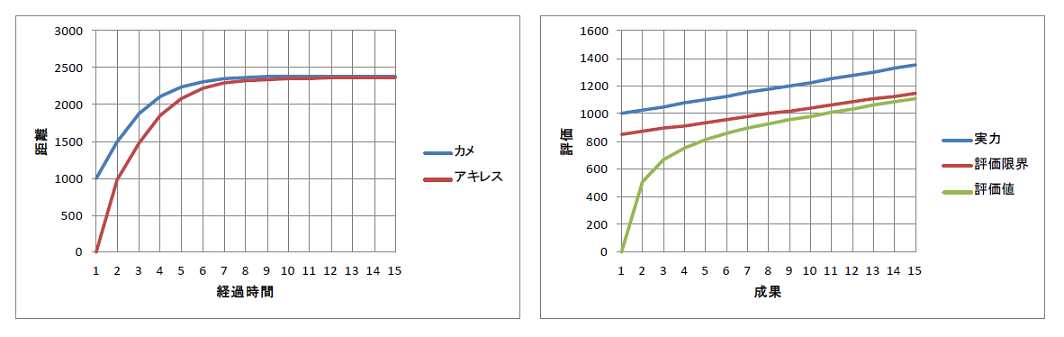
　左側のグラフはアキレスとカメの関係です。 この関係を参考に、人の評価をモデリングした関数が右側のグラフです。 以下がその評価式です。
　　　
右側の式から、成果に比例して評価値は評価限界に近づく性質があることが分かります。 人は相手を自分よりも高くは評価できません。 よって、組織の中で人を引き上げるならば、より上の人間が評価しなければならないということです。

　ここで、評価式について補足します。 まず、人は自分を上回らないように調整して相手を評価します。 このときの評価限界はそのときの実力に比例します。 ただ、評価者も成長しており、評価限界も向上します。 この評価限界に無限に近づく関数として、成果の逆数に注目します。
　　　
評価限界に近づくようにこの関数のスケールは評価限界とし、近づき方を指数のaで調整します。 差分を評価値として式変形することで、評価値を算出できます。