ActionData↑

損益分岐点

　損益分岐点とは、活動に対する経費と売上が一致する点のことです。 そもそも事業は、経費よりも売上が上回っていなければ継続することができません。 言い換えれば、事業を継続させるためには、損益分岐点を越えなければならないということです。 以下、活動に対する経費と売上の関係の例です。

　　　

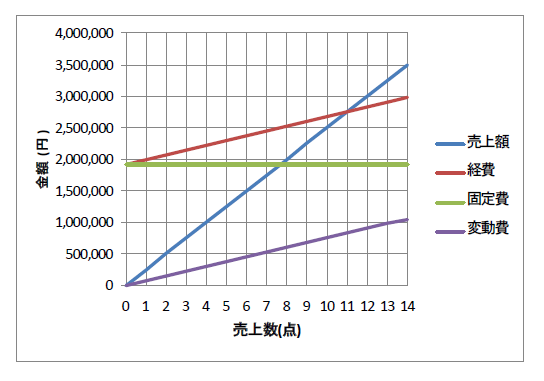
経費と売上が一致する点とは、経費と売上が交わっている点であり、この交点が損益分岐点となります。 このように活動に対する経費と売上から損益分岐点を求める分析をCVP分析(損益分岐点分析)と言います。 この例の場合、活動とは売上数を指します。 もし、月単位で特定の商品に対して分析したということであれば、この商品は毎月11点以上は売らなければならない商品ということが分かります。

データから損益分岐点を求める場合

　ここではデータがある場合を想定し、その損益分岐点を求めます。 つまり、既存の事業に対する損益分岐点を求めます。 これを最低限の努力目標とします。 ただし、通常、努力目標は損益分岐点よりやや高めに設定します。 以下、データから損益分岐点を求める手法です。

　　　

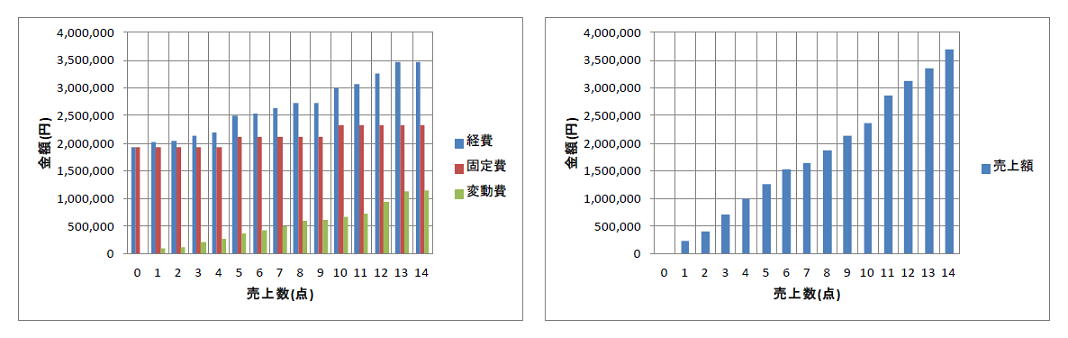
左側のグラフは経費に関するデータで、右側は売上額のデータです。 それぞれ回帰分析することで、以下のような、経費の回帰式と売上額の回帰式が得られます。
　　　
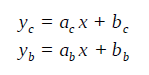
経費の回帰式(上側の式)において、傾きを変動費、切片を固定費とします。 それら回帰式の交点を損益分岐点とします。 まとめると以下の手順のようになります。

　　　【手順１】経費に関するデータを集計し、回帰分析する。
　　　　　　　　これにより、以下のような回帰式を得る。
　　　　　　　　　　y = ax + b
　　　　　　　　※aが変動費であり、bが固定費である。
　　　【手順２】売上についても同様にデータを集計し、回帰分析し、回帰式を得る。
　　　【手順３】手順１で得た回帰式と手順２で得た回帰式の交点を求め、損益分岐点とする。

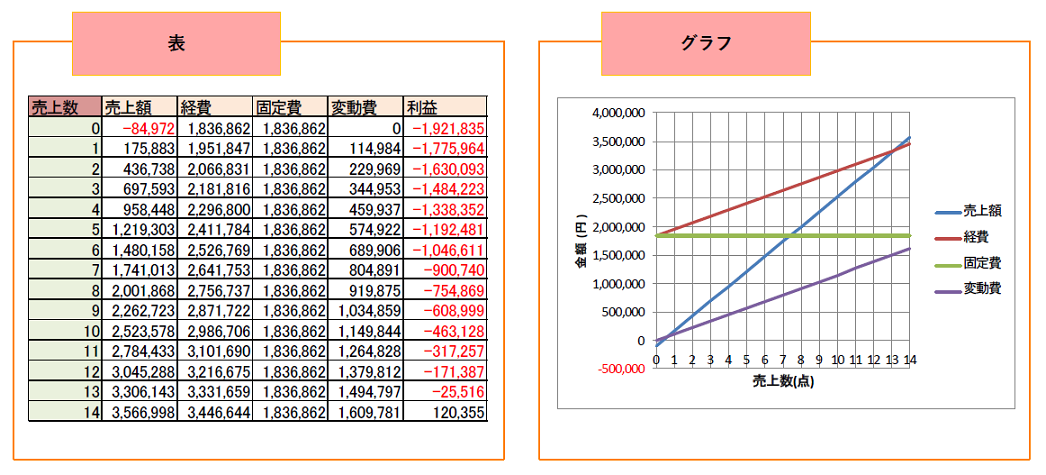
　これらの手順を踏まえ、データから既存の事業の損益分岐点を求めます。 以下は、売上と経費を月単位で管理している場合において、とある商品の1ヵ月間における売上額と経費からCVP分析した結果です。 売上額と経費は、それぞれのデータを回帰分析して得られる回帰式による推定値です。 固定費は回帰式の切片ですが、これは、売上数に関係なく1ヵ月間で発生する費用を意味します。 表より、利益がプラスに転じる点(損益分岐点)は、売上数が14点のときだと分かります。 つまり、該当の商品は毎月14点以上は売らなければならない商品ということです。

　　　

計算によって損益分岐点を求める場合

　ここではデータがない場合を想定し、その場合の損益分岐点を求めます。 例えば、新規事業を立ち上げる場合がこれにあたります。 新規事業のためデータは存在しません。 しかし、投資した分を回収するためにはどれだけ稼がなければならないかを計算する必要があるため、損益分岐点は算出しなければなりません。 以下、データがない場合に、計算によって損益分岐点を求める手法です。

　　　

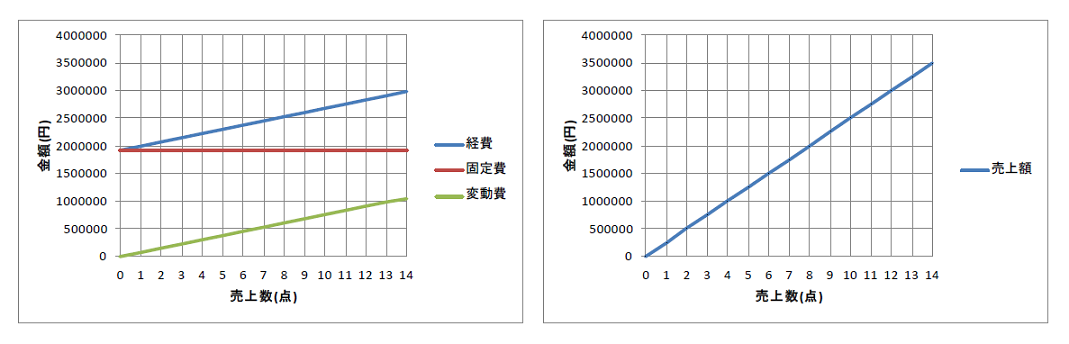
データがないため、回帰分析して損益分岐点を求めることはできません。 よって、予想されるデータを計算によって求め、損益分岐点を算出します。 上の左側のグラフは経費に関する予想で、右側は売上額の予想です。 商品がn個売れた際の経費と売上額を計算して、予想とします。 そうして、経費と売上額が一致する点、つまり、経費の直線と売上額の直線の交点を損益分岐点とします。 もしくは、今回の場合は以下のようにしてもかまいません。
　　　
まとめると以下の手順のようになります。

　　　【手順１】事業の投資額(立ち上げに際し発生した費用および当分の運転資金)を固定費として集計する。
　　　　　　　　※計算によって求めたデータを用いる。
　　　【手順２】商品あたりの売上額と経費を集計する。経費は変動額に相当する。
　　　　　　　　※計算によって求めたデータを用いる。
　　　【手順３】固定費と変動費の和が売上額と一致する点を求め、損益分岐点とする。

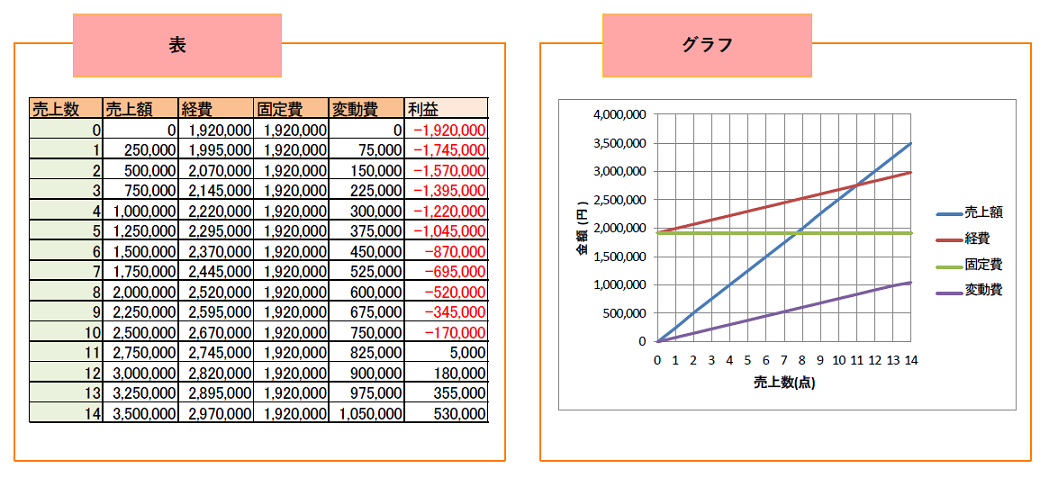
　これらの手順を踏まえ、計算により新規事業の損益分岐点を求めます。 新規事業として、単価25万円で原価7.5万円の新商品を開発しました。 初期投資および運転資金は192万円で、これは固定費に相当します。 そうして単価と売上数の積を売上額、原価と売上数の積を変動費とし、CVP分析した結果が以下です。 表より、利益がプラスに転じる点(損益分岐点)は、売上数が11点のときだと分かります。 つまり、11件の契約を獲得できれば、該当の商品の開発プロジェクトは元が取れたということになります。

　　　

【補足】上限の損益分岐点

　通常、損益分岐点は超えるべき点です。 しかし、超えてはいけない点としての損益分岐点も存在します。 一般的に、損益分岐点は2本の直線の交点として求められます。 直線であるため、利益を出せる領域は開いているように見えます。 しかし実際は、売上も経費も直線とはならず、領域は閉じています。 売上が無限に増えるようなことはなく、逆に経費は指数的に増えるためです。 以下、上限の損益分岐点とその曲線について説明します。

　　　

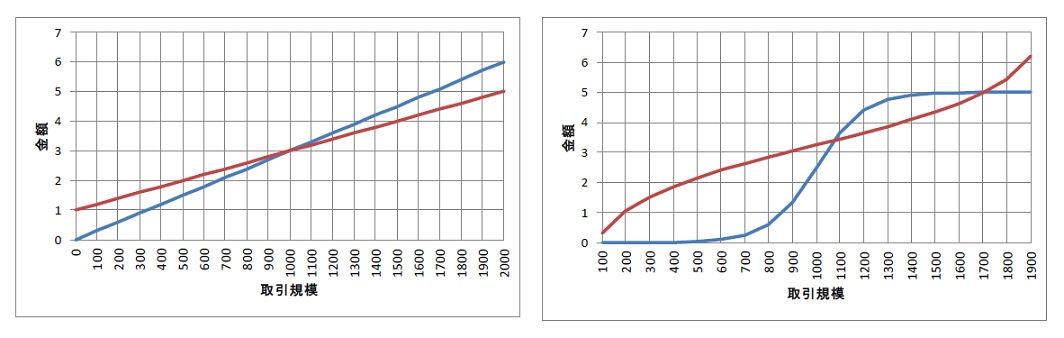
左側のグラフは直線で求めた損益分岐点であり、右側のグラフは曲線で求めた損益分岐点です。 右側のグラフにおいて、青色の曲線が売上を表すシグモイド関数で、赤色の曲線が経費を表すロジット関数です。 下限と上限の2つの交点が存在し、この閉じた領域内でしか利益を生み出せないことを表しています。 上限の損益分岐点を求めるにあたって、曲線でモデリングすることは面倒なため、直線でモデリングします。 やり方として、データがある場合とない場合に分かれます。