ActionData↑

適正在庫数

　不良在庫を恐れ在庫数を抑えると、欠品の可能性が高くなり、店舗の魅力が損なわれかねません。 逆に過剰に仕入れると、在庫の管理コストが圧迫し、キャッシュフローが悪化します。 特にアパレルショップの場合、１種類の商品に対して、異なるサイズの在庫を管理する必要があります。 および、季節の移り変わりも意識しなければなりません。 これらの点を考慮し、以下のように適正在庫数を求めます。

　　　

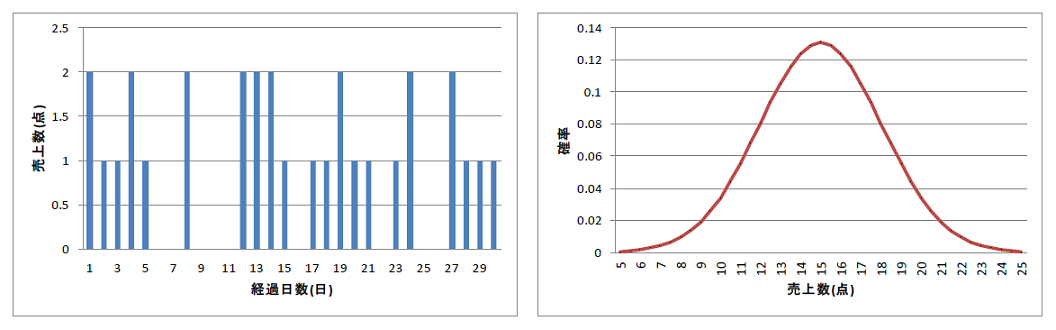
左側(青色)のグラフは、指定の商品の直近の1ヵ月間における日別の売上数の推移です。 対して右側(赤色)のグラフは、一定の期間(リードタイムや保管期間を指定)における売上数の予想の分布です。 中心極限定理より、分布は正規分布とします。 ここで、売れる季節を考慮し、在庫の保管期限を定めます。 この期限を過ぎた在庫は廃棄します。 よって、欠品率(在庫数以上に売れる確率)と廃棄率(期間以内に売り切れない確率)を抑えるよう、仕入れしなければなりません。 まずは、欠品率と廃棄率を求めます。 その上で最適な在庫数(適正在庫数)を求めます。

一般的に適正在庫数は、安全在庫数に余剰分を加えて求めます。 安全在庫数は、以下の式で求められます。
　　　
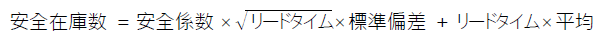
安全係数は標準正規分布の統計量のため上記のような式となっています。 しかし実は、正規分布の統計量は標準化しなくても求めることができるため、実際に安全在庫数を求めるにあたって上記の数式を意識することはありません。

　　　

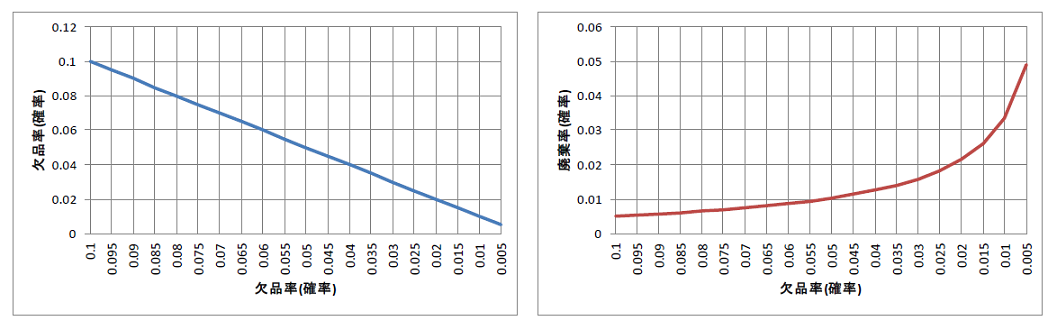
左側(青色)のグラフは、単純に欠品率の推移であり、右側(赤色)のグラフは、欠品率に対する廃棄率の推移です。 これらはトレードオフの関係で、例えば、欠品率を下げると廃棄率が上がってしまいます。 ここで、期待値を以下のように欠品数と廃棄数の和として定義します。 この期待値が最小となる在庫数を適正在庫数と定めます。 まとめると以下の手順のようになります。

　　　【手順１】商品ごとに、直近の一定の期間の売上数の推移を集計する。
　　　　　　　　※ここでは直近の1ヵ月間の日別の売上数の推移を集計する。
　　　【手順２】集計した売上数から所定の統計量を計算し、一定の期間における売上数の予想の分布を導出する。
　　　　　　　　※リードタイムにおける分布と、保管期間における分布を導出する。
　　　【手順３】リードタイムにおける分布から欠品率を、保管期間における分布から廃棄率を求める。
　　　【手順４】欠品率を変化させたときの廃棄率を求める。
　　　　　　　　そして、欠品率と廃棄率から期待値を計算する。
　　　【手順５】期待値が最小となる在庫数を探索し、適正在庫数とする。
　　　【手順６】他に制約がないか確認した上で、適正在庫数を確定する。
　　　　　　　　※例えば、スペースの問題や棚卸の問題など。

適正在庫数の算出

　アパレルショップを想定し、特定の季節物の商品における適正在庫数を算出します。

　　　

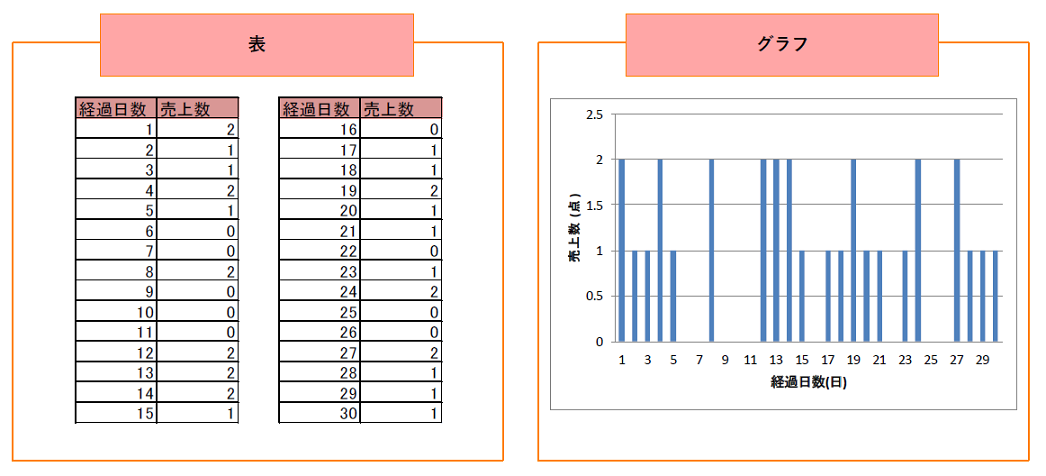
表は、指定の商品の直近の1ヵ月間における日別の売上数の推移です。 グラフより、1日1個程度売れている様子が分かります。 つまり、集中的に売れる商品ではなく、毎日一定数売れる商品ということです。 この商品の平均は1.00で、標準偏差は0.79です。 これらの統計量より、リードタイムにおける分布と保管期間における分布を導出し、欠品率と廃棄率を求めます。

　　　

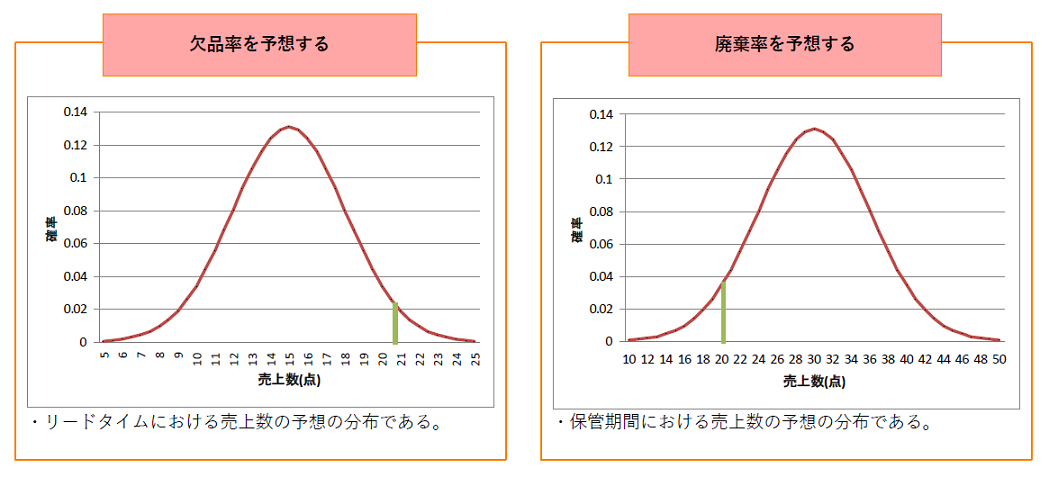
リードタイムを15日、保存期間は30日としており、15日以内に在庫数以上売れる確率(左側の分布の緑線より右側の確率)が欠品率となり、30日以内に売り切れない確率(右側の分布の緑線より左側の確率)が廃棄率となります。 仮に、欠品率を5%としたときの在庫数は21点であり、廃棄率は1%となります。 もし欠品率を1%にまで下げると廃棄率は3%となります。 このように欠品率を変化させ、欠品率も廃棄率も抑えられるような在庫数を探索します。

　　　

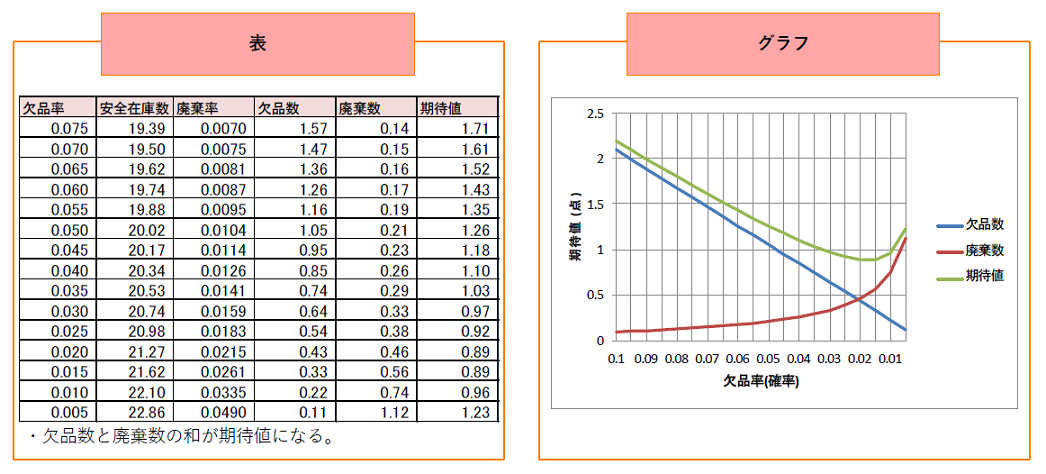
欠品率と廃棄率より期待値を計算した結果、表とグラフのようになりました。 表より、欠品率が0.02のとき、期待値が最小になることが分かります。 このときの在庫数は22点で、これが適正在庫数となります。 ここでは取り扱いませんでしたが、もし曜日によって売れ方が異なる(標準偏差が異なる)のであれば、分布の導出の仕方は工夫しなければなりません。 他、リードタイム短縮、スペース節約、棚卸頻度の低減の観点からも在庫の在り方を検討します。