組織管理へ応用
品質管理
- ・品質管理について例を挙げてご説明します。
- ・統計的検定により、商品・サービスの品質をチェックします。
- ・不明点あれば問い合わせください。
- ※当サイトで掲載しているデータは適当に作成したものであり、実際のものではありません。
初回の提供時間
飲食店では、来店者の初回の注文は特に迅速に対応しなければなりません。
ただし「何分以内に対応する」というような目標値を設定しても、注文内容によっては目標値を守れません。
よって、単純に全店舗と比較することで遅いかどうか判断します。
今回の場合、店舗Aの平均が全店舗の平均を上回っていなければいいため、以下の通り、スチューデントのt分布による片側検定(右)を実施します。
【手順1】事前に、全店舗の初回の提供時間をサンプリングし、その平均を割り出しておく。
【手順2】店舗Aにおける初回の提供時間をサンプリングし、その平均を割り出す。
※ここではサンプル数は10
【手順3】所定のパラメータを算出する。
【手順4】t分布に当てはめ、店舗Aの平均が全店舗の平均と一致しているか検定する。
店舗Aにおける初回の提供時間をサンプリングした結果、以下のようになりました。
初回の提供時間とは、初回の注文からその商品を提供するまでの時間です。
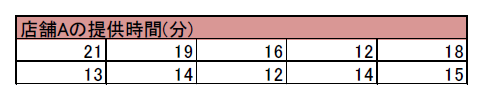
これに対して、全店舗の平均は14.8分です。
この点を踏まえ、所定のパラメータを算出しt検定すると、以下のような結果になります。

※有意水準は5%
統計量が限界値(上)より小さいことから、統計量は棄却域になく、店舗Aの平均が全店舗の平均と一致しているという仮説は棄却されません。
よって今回の場合は、店舗Aの初回の提供時間は遅くはないと判断できます。
日替わり定食の提供時間
引き続き飲食店にて、日替わり定食は提供時間の短縮を目指しており、提供時間の目標値を設定しています。
その効果を確かめるため、店舗Aの提供時間が設定した目標値と比較して遅くないか調査します。
今回の場合、店舗Aの平均が目標値を上回っていなければいいため、以下の通り、スチューデントのt分布による片側検定(右)を実施します。
【手順1】事前に、日替わり定食の提供時間の目標値を設定しておく。
【手順2】店舗Aにおける日替わり定食の提供時間をサンプリングし、その平均を割り出す。
※ここではサンプル数は10
【手順3】所定のパラメータを算出する。
【手順4】t分布に当てはめ、店舗Aにおける日替わり定食の平均が目標値と一致しているか検定する。
店舗Aにおける日替わり定食の提供時間をサンプリングした結果、以下のようになりました。
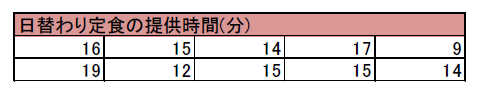
これに対して、日替わり定食の目標値は10分です。
この点を踏まえ、所定のパラメータを算出しt検定すると、以下のような結果になります。

※有意水準は5%
統計量が限界値(上)以上であることから、統計量は棄却域にあり、店舗Aの日替わり定食の平均が目標値と一致しているという仮説は棄却されます。
よって今回の場合は、店舗Aの日替わり定食の提供時間は目標値と比較して遅いと判断できます。
食べ残しの量
食べ残されたということは、味が悪いということを意味していると捉えられます。
よってまずは、売れ筋商品の定食において、食べ残しの量が過去と比較して増えてないか調査します。
今回の場合、先週の平均が過去データの平均を上回っていなければいいとして、以下の通り、スチューデントのt分布による片側検定(右)を実施します。
【手順1】事前に、店舗Aにおける定食の過去の食べ残しの量をサンプリングし、その平均を割り出しておく。
【手順2】店舗Aにおける定食の先週の食べ残しの量をサンプリングし、その平均を割り出す。
※ここではサンプル数は10
【手順3】所定のパラメータを算出する。
【手順4】t分布に当てはめ、店舗Aにおける先週の平均が過去の平均と一致しているか検定する。
店舗Aにおける定食の先週の食べ残しの量をサンプリングした結果、以下のようになりました。
ここでは単位を点(商品数)としてカウントしています。

これに対して、過去の定食の食べ残しの平均は94点です。
この点を踏まえ、所定のパラメータを算出しt検定すると、以下のような結果になります。

※有意水準は5%
統計量が限界値(上)より小さいことから、統計量は棄却域になく、店舗Aの先週の平均が過去の平均と一致しているという仮説は棄却されません。
よって今回の場合は、店舗Aの定食の食べ残しの量は増えてないと判断できます。
ステーキの量
ステーキ定食のステーキはその場で料理人がさばいています。
量が少なすぎればクレームとなり、逆に量が多すぎれば損失となります。
そこで、さばかれた肉の量が均一になっているか調査します。
今回の場合、標準偏差の目標値を10とし、このばらつきを上回っていなければいいとします。
この点を踏まえ、以下の通り、カイ二乗分布による片側検定(左)を実施します。
【手順1】事前に、ステーキの量の標準偏差の目標値を設定しておく。
【手順2】店舗Aにおけるステーキの量をサンプリングし、その分散を割り出す。
※ここではサンプル数は10
【手順3】所定のパラメータを算出する。
【手順4】カイ二乗分布に当てはめ、店舗Aにおけるステーキの量の分散が目標値以下であるか検定する。
店舗Aにおけるステーキ定食のステーキの量をサンプリングした結果、以下のようになりました。

これに対して、ステーキの標準偏差の目標値は10です。
この点を踏まえ、所定のパラメータを算出しt検定すると、以下のような結果になります。

※有意水準は5%
統計量が限界値(下)以下であることから、統計量は棄却域にあり、店舗Aのステーキの分散が目標値と一致しているという仮説は棄却されます。
よって今回の場合は、店舗Aのステーキのばらつきは目標値と比較して少ないと判断できます。
汁物の温度
味は温度に関係します。
そして、温度は冷めやすいものです。
汁物の場合は、そうした点に注意して提供しています。
汁物の品質の検査として、提供する汁物の温度にばらつきがないか調査します。
今回の場合、標準偏差の目標値を3とし、このばらつきを上回っていなければいいとします。
この点を踏まえ、以下の通り、カイ二乗分布による片側検定(左)を実施します。
【手順1】事前に、汁物の温度の標準偏差の目標値を設定しておく。
【手順2】店舗Aにおける汁物の温度をサンプリングし、その分散を割り出す。
※ここではサンプル数は10
【手順3】所定のパラメータを算出する。
【手順4】カイ二乗分布に当てはめ、店舗Aの汁物の温度の分散が目標値以下であるか検定する。
店舗Aにおける汁物の温度をサンプリングした結果、以下のようになりました。

これに対して、汁物の温度の標準偏差の目標値は3です。
この点を踏まえ、所定のパラメータを算出しt検定すると、以下のような結果になります。

※有意水準は5%
統計量が限界値(下)以下であることから、統計量は棄却域にあり、店舗Aの汁物の温度の分散が目標値と一致しているという仮説は棄却されます。
よって今回の場合は、店舗Aの汁物の温度のばらつきは目標値と比較して少ないと判断できます。