ActionData↑

コンジョイント分析とは

　コンジョイント分析とは、主に商品企画で利用される分析で、膨大な組み合わせから望ましい組み合わせを効率良く特定する分析です。 元々は実験計画法という統計的な手法であり、コンジョイント分析とは、実験計画法をマーケティングに拡張した手法です。 実験計画法とは、膨大な組み合わせを伴う実験を効率良く実施するために考案された、実験の計画の立案とその結果の分析に関する手法です。 膨大な組み合わせを伴う実験は数多く存在し、農学、医学、工学、心理学など、実験計画法は幅広い分野で利用されています。

　同様に、商品企画でも膨大な組み合わせを試行しなければなりません。 コンジョイント分析はこの点に着目し、効率良く商品企画を行う方法として定着しました。 商品企画であれば、それを受け入れるのは消費者である以上、どのような商品が望ましいか、正解を知っているのは消費者と言えます。 となれば、調査すべきは消費者ということになります。 よって、実験計画法が実験結果を分析していたことと同様に、コンジョイント分析では消費者からの何らかの回答(アンケートなど)を分析します。 そうして、消費者の意見を取り入れつつ、効率良く商品企画する方法がコンジョイント分析です。

コンジョイント分析のやり方

　コンジョイント分析する大雑把な手順を以下に示します。

　　　【手順１】属性と水準を明確化する。
　　　【手順２】属性と水準に適した直行表を選定する。
　　　【手順３】直行表に当てはめ計画を立案する。
　　　【手順４】順次、実施し、その結果(評価)を記録する。
　　　【手順５】結果を指定の方法により分析する。
　　　※属性と水準の影響度を明確化する。
　　　【手順６】分析された結果をグラフ化する。

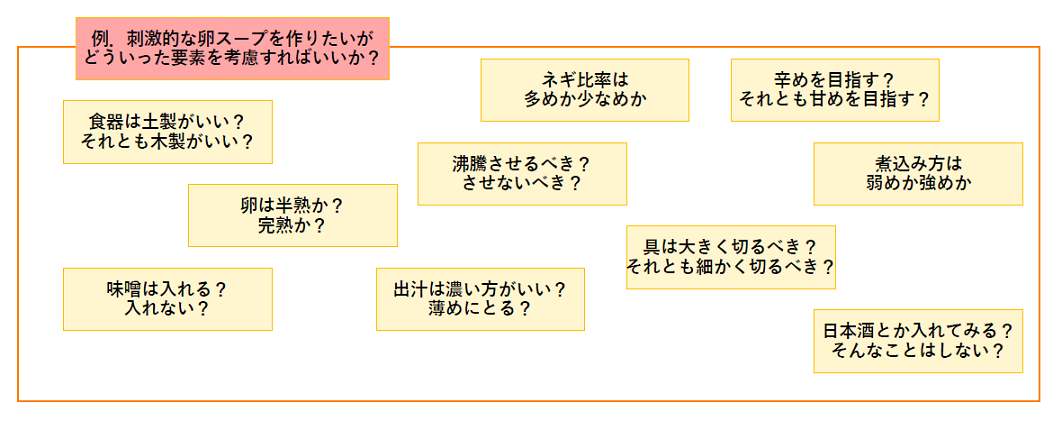
まず、属性と水準を明確化します。 これは、目的と取り得る手段の組み合わせを考えることに相当します。 以下に、卵スープを作ることを目的とした際の取り得る組み合わせの例を示します。

　　　　　　　卵：　半熟、完熟
　　　ネギ類比率：　少なめ、多め
　　　　　切り方：　小さく切る、大きく切る
　　　　煮込み方：　弱く、強く
　　　　　　味噌：　無し、有り
　　　　　　沸騰：　沸騰させない、沸騰させる
　　　　　　　酒：　無し、有り

左側のカテゴリを属性、右側のメンバを水準と言います。 これは実験計画法(コンジョイント分析)の言い方です。 このような属性と水準に対して、適切な直行表を選定します。 直行表の形はあらかじめ決まっており、形状が最も近いものを採用します。 今回は以下の2水準7属性の直行表を採用します。

　　　

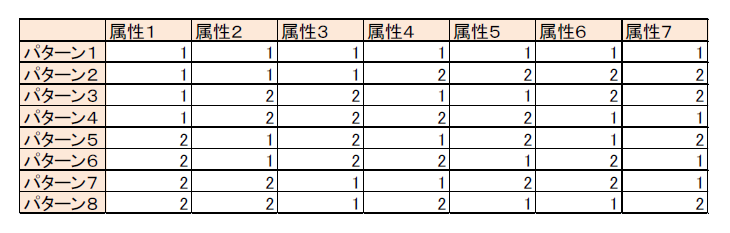
この直行表に対して以下のように当てはめます。

　　　

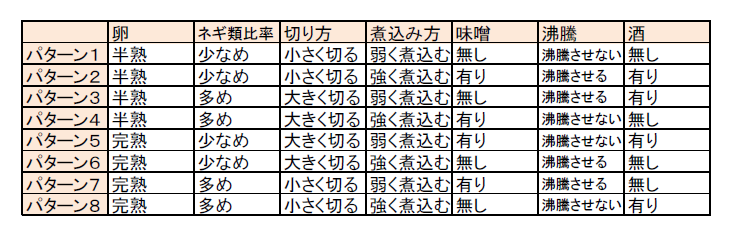
そしてパターン1からパターン8までを順に実施していきます。 実際に直行表のパターンで卵スープを試作し、試作した卵スープを試食してもらい、3段階評価(1:不味い、2:普通、3:美味い)を付けてもらうようにします。 この組み合わせで実施することで、全パターン(128パターン)を実施せずとも、理論上は全パターンを網羅したことになります。

　　　

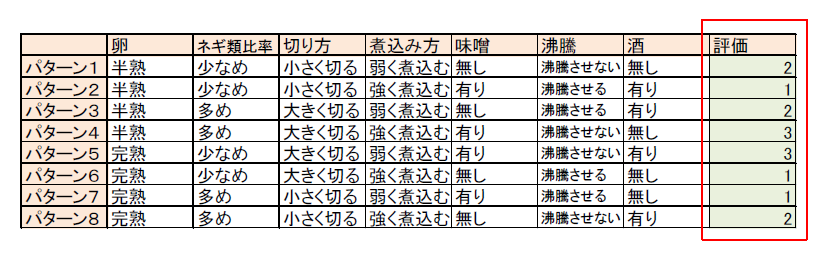
そうして全8パターンの結果(評価)が揃ったところで実験は終了です。 ここで、結果は目的変数であり、水準は説明変数に相当します。 この点を踏まえ、水準が結果に与える影響を調査するため、これらを回帰分析します。 ただし水準は質的変数のため、分析は数量化1類となります。 回帰式を推定できたところで、属性と水準の影響度(重要度)を計算し、グラフ化します。

　　　

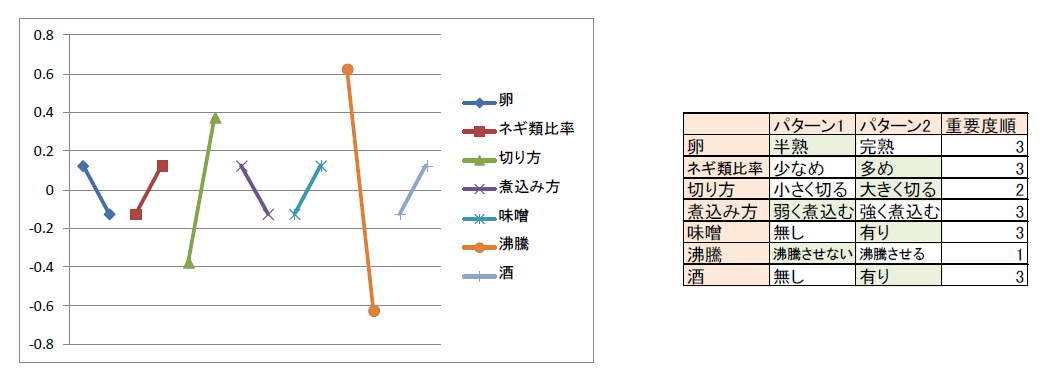
分析結果より、「沸騰」が最も影響が大きく、次に「切り方」が影響していることが分かります。 そして、「沸騰」と「切り方」以外はすべて同じ影響度であるということが分かります。 つまり考慮すべきはまずは「沸騰させるかさせないか」からということです。 一方、水準についてですが、「沸騰」は右下がりで、「切り方」は右上がりです。 よって、「沸騰」は「させない」方が良く、「切り方」は「大きく切る」方が良いということが分かります。 これらの最適な組み合わせは表の通りです。

コンジョイント分析の特徴

　コンジョイント分析を用いることで、実施すべきパターン数を大幅に減らすことができます。 というのも、直行表の組み合わせであれば、他の水準の影響を平均によって除外することができ、表れた差分から水準の影響を特定できるためです。 これにより、組み合わせの全パターンを実施せずとも、直行表における全パターンを実施するだけで、あらゆる組み合わせの結果を予測できるようになります。 さきほどの卵スープを例にとりますが、以下の図の観点で全パターンを考慮しようとしただけでも、計1024パターンを試さなければならなくなります。 とても網羅できる数ではありません。 しかし、コンジョイント分析することによって、現実的な実施回数で理論上は全パターンを網羅できるようになります。

　　　

コンジョイント分析の利点

　コンジョイント分析では回帰分析を利用します。 回帰分析することで、説明変数の目的変数に対する影響度を数値化できるためです。 未知の変数を予測するだけが回帰分析ではありません。 そして、商品企画するにあたって知りたいことは、「何が売上に影響しているか」です。 それは水準が結果に与える影響、ということに他なりません。 このためコンジョイント分析では、回帰分析を利用して水準の影響度を推定します。 こうして属性や水準の影響度を調査し、影響の大きな要素を優先的に考慮することにより、効率的に商品企画できるようになります。

　一般的に商品企画では、調査・発想・試作・評価・反省といったプロセスを繰り返します。 しかし評価・反省は、評価・反省する人の「好き嫌い」や「理解できるできない」によって、大きく左右されるものです。 結果として売れたヒット作品も、企画当初は社内では売れないと言われ続けた、ということはよくある話です。 商品企画において本当に必要なものは消費者の声であり、実際のところ社内の人間の意見に価値はありません。 しかしながら、商品企画に協力してくれる消費者はそうそう見つからず、社内の人の意見を介して消費者の声を探っているのが実状です。 こうした中であっても、コンジョイント分析を利用することで、可能な限り消費者の意見に近づけた評価ができるようになります。

コンジョイント分析の活用例

　最後にコンジョイント分析の活用列をいくつか挙げておきます。

新商品開発(デスク)：
家具工場にて、新商品(デスク)の開発をしているところです。 お客様はどのようなデスクを欲しがっているのか、コンジョイント分析して調査することにしました。 コンジョイント分析するにあたって、属性と水準は以下のように設定しました。
　　　　色：　白、黒、茶色
　　　　形：　長方形、楕円形
　　　素材：　木製、金属製
　　　質感：　重い、軽い
　　　重視：　機能性、デザイン
　　　高さ：　固定、調整可能
評価として、お客様にアンケートを依頼しました。 直行表に従いパターンを提示し、どの商品を購入するか回答してもらいました。 購入するパターンを1種類だけ選択してもらい、評価値は購入人数としました。

店舗デザイン：
新店をオープンさせる予定の飲食事業者にて、新店のデザインを考案しているところです。 お客様がどのようなデザインを好むのか、コンジョイント分析して調査することにしました。 コンジョイント分析するにあたって、属性と水準は以下のように設定しました。
　　　店員の年代：　～20代、30代、40代～
　　　店員の性別：　男性、女性
　　　　　　　色：　白系、黒系
　　　　　明るさ：　明るい、暗い
　　　　　雰囲気：　賑やか、静か
　　　　　タバコ：　全面禁煙、一部喫煙可
　　　　　建築物：　木造、鉄筋コンクリート
　　　　　　立地：　ロードサイド、駅周辺
評価として、お客様にアンケートを依頼しました。 直行表に従いパターンを提示し、3ヵ月で何回来店したいか回数を回答してもらいました。 評価値はそのまま回数としました。

スピーチ練習：
大学でスピーチの練習をしているところです。 スピーチ力を向上させるために、どのような点を意識すべきか、コンジョイント分析して調査することにしました。 コンジョイント分析するにあたって、属性と水準は以下のように設定しました。
　　　　　　　　声：　落ち着きある声、語りかける様
　　　　　　　視線：　あまり動かさない、動かす
　　　ジェスチャー：　付ける、付けない
　　　　　　　服装：　白系、黒系
評価として、視聴者に印象を3段階評価してもらいました。 評価値はそのまま3段階評価の点数(0,1,2)としました。