ActionData↑

回帰分析とは

　回帰分析とは、最小二乗法を利用し残差の分散を最小化することで、尤もらしい近似関数を導出する分析手法です。 言い方を変えると、既知の説明変数(独立変数)と目的変数(従属変数)のデータから、関係性を明確化し、未知の変数を説明する(関数の係数を導出する)分析手法ということです。 通常、経営において回帰分析というと、単回帰分析を指します。 対して、理系の分野で回帰分析というと、重回帰分析(数量化1類)を指します。 以下、大雑把に特徴を挙げておきます。

　　　単回帰分析：
　　　・説明変数が1種類の場合の最も基本的な回帰分析です。
　　　・1次直線で近似されることが一般的です。
　　　・直線があるがゆえ最も理解しやすく、よってこの形の分析は多々あります。

　　　重回帰分析：
　　　・単回帰分析と比較して説明変数が2種類以上の場合の回帰分析のことです。
　　　※考え方は単回帰分析と同様です。
　　　・意図的に絞らなければ説明変数は複数存在するため、実際は重回帰分析の方が重宝します。

　　　数量化1類：
　　　・数値以外(質的変数)を対象とした回帰分析のことです。
　　　※考え方は回帰分析と同様です。

　回帰分析は近似関数を導出する分析手法です。 データの分類は行いませんが、変数間の関係性を明確化し、未知の変数の予測や構造の数値化が可能です。 未知の変数を予測できるということは、試していない組み合わせであってもそれらしい数値を計算できるということです。 このため売上予想や株価予想といった、未来の予想でも活用されています。

　冒頭で説明した最小二乗法は、残差の分散を最小化し近似関数を導出する数学的な手法の一つです。 基本的に回帰分析では1次関数で近似しますが、最小二乗法に当てはめれば、どんな形の関数ででも近似することができます。 ここでは1次関数もしくは分数関数でのみ近似するようにします。 あまり複雑に分析しても経営戦略や組織管理へは応用できないので、複雑になりすぎないように注意しなければなりません。 以下、1次関数(左側)と分数関数(右側)で回帰分析したイメージです。

　　　

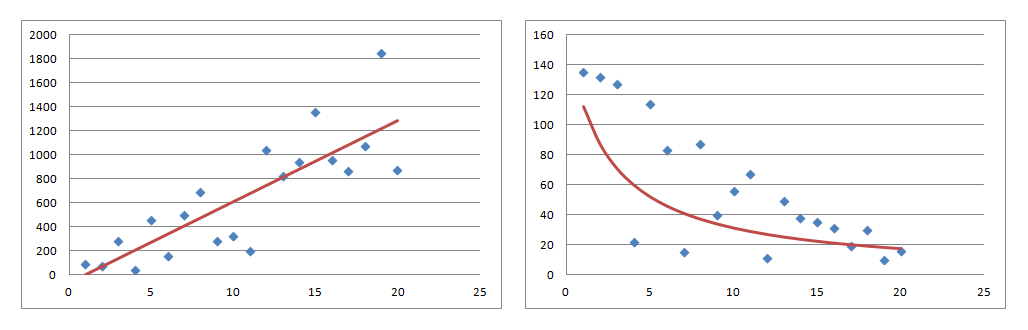
回帰分析のやり方

　まず、分析対象とするデータを用意します。 以下にデータ(業務管理システムの売上と経費に関するデータ)の例を示します。

　　　

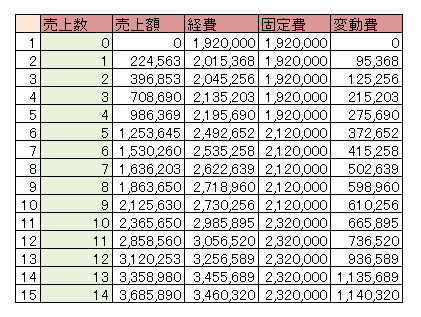
このようなデータに対して、以下のような手順で分析を進めていきます。

　　　【手順１】目的変数を決定します。
　　　【手順２】説明変数を決定します。
　　　【手順３】係数を算出します。
　　　【手順４】導出された回帰式に問題ないか検証します。
　　　※もし問題あればデータを調整し再計算します。

　回帰式を導出できたところで分析は終了です。 後は、導出された回帰式に対して、原因の考察と対応を考えていくのみです。 以下、上記の手順で分析した例です。 今回は売上数から売上額と経費を予想したいため、説明変数は売上数で、目的変数は売上額と経費になります。 そうして回帰分析して得られる回帰式より売上額と経費を推定します。

　　　

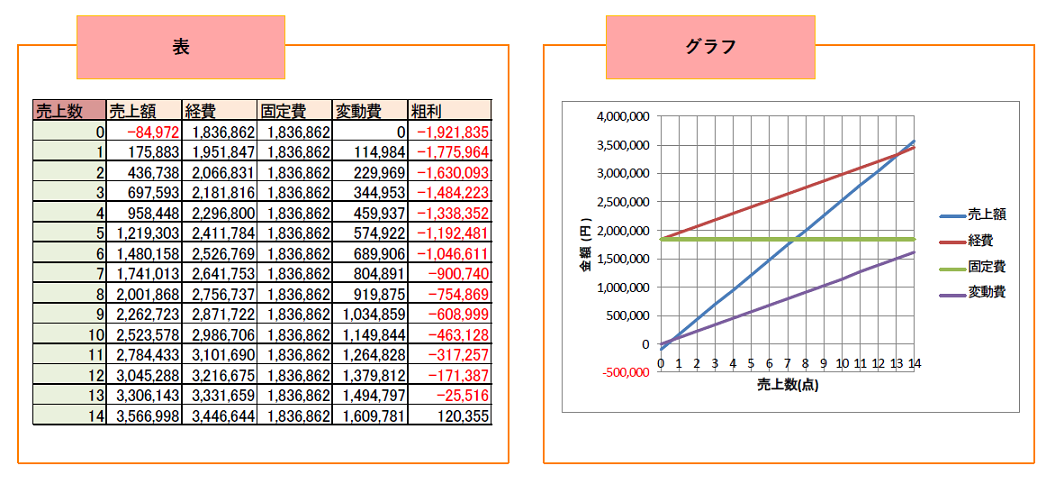
分析結果より、粗利がプラスに転じる点(損益分岐点)は、売上数が14点のときだと分かります。 ここで、今回、分析対象としたデータは、とある商品における1ヵ月間の売上と経費に関するデータです。 1ヵ月間となっているのは、損益を月単位で管理しているためです。 つまりこの商品は、1ヵ月間で14点は販売しなければ利益が出ない商品、ということです。

　ここで、回帰分析するにあたって、「相関係数」と「決定係数」という二つの指標があります。 相関係数は説明変数と目的変数の相関関係の強さを表現した指標で、-1～1の値をとります。 0は相関がない(全体的に散らばっている)ことを示し、|1|は強い相関があることを示しています。 また、1が正の相関(右上がり)で、-1が負の相関(左上がり)です。 対して決定係数は、回帰式が説明できる精度を示す指標であり、相関係数を2乗した値です。 よって、決定係数は0~1の値をとります。 例えば、相関係数が0.7であれば決定係数は0.49となります。 決定係数は0.5以上が望ましいため、相関係数が0.7を下回る場合は、あまり回帰式は利用しない方がいいと言えます。

回帰分析の特徴

　回帰分析は、数値解析する分析手法としては、極めて応用範囲の広い分析です。 というのも、分析結果が複雑にならず、誰が見ても何が言いたいのか直感的に理解できるためです。 そして、未来予測や構造の明確化という比較的重要な点を、簡単な手順で尤もらしい値として推定することができます。 また、最小二乗法から組み立てられれば、重み付きで回帰分析するようなこともできます。 サンプリングされたデータに重みを考慮したい場合に有効です。

　ここまで、単回帰分析を前提に話を進めてきました。 もし重回帰分析になると、説明変数の数だけ回帰式が導出されるようになります。 よって、連立させて回帰式を解き回帰係数を求めることになります。 連立方程式をプログラムで解くにあたっては、行列による記法が便利です。 説明変数が2種類程度であれば問題ありませんが、これが10種類、100種類と増えていくと、よりシンプルな記法が好まれます。 このため、連立方程式となった場合は、逆行列を求めることで回帰係数を求めていきます。

　ここで、もし説明変数間に強い相関がある場合は、一方の説明変数は不要、ということになります。 そうなると、逆行列を求めることができなくなります。 これを多重共線性(俗にマルチコ)と言います。 連立方程式を解くにあたって、式の数は変数の数よりも多くなければなりません。 もし多重共線性が起こった場合は、説明変数を選びなおして、再度分析する必要があります。 Excelを利用した分析でも発生する現象であり、説明変数の選定には注意が必要です。

回帰分析の利点

　回帰分析することで、未知の変数を予測でき、かつ、構造を数値化することができます。 また、回帰分析は計算コストも低いため、ビッグデータの解析手法としても応用されています。 および、最小二乗法が考えの基本であり、改良しようと思えば自由にカスタマイズすることができます。 例えば、商品・サービスが売れる変化は直線ではなくシグモイド関数です。 同様に、コストが発生する変化も直線ではなくロジット関数です。

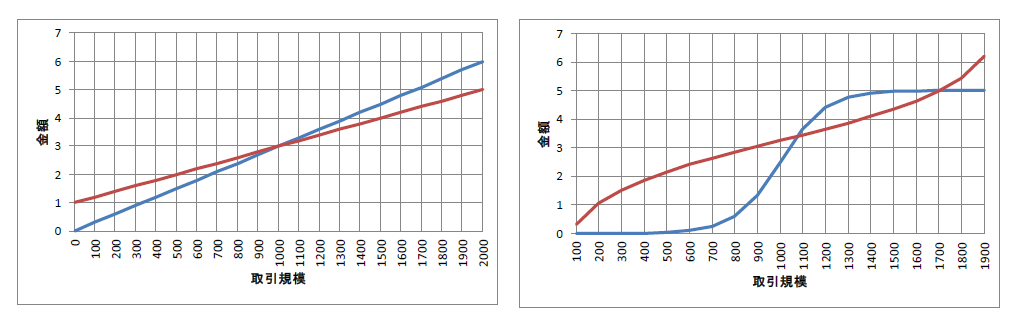
　一般的にはどちらも直線で捉えられがちですが、実際のところ、どちらも直線ではありません。 回帰分析は簡略化して直線で行いますが、より現実に即したモデルで分析する場合は、曲線で近似しなければなりません。 以下、直線で近似したグラフ(左側)と曲線で近似したグラフ(右側)のイメージです。 青線が売上で赤線が経費(コスト)です。 特に、右側のグラフの青線がシグモイド関数で、赤線がロジット関数です。

　　　

　ここまで、説明変数は量的変数という前提で話を進めてきました。 単回帰分析にしろ重回帰分析にしろ、説明変数は量的変数であることを前提としています。 もし説明変数が質的変数であれば、単純に回帰分析できないため、数量化1類の操作を行います。 そうして質的変数な説明変数を量的変数に変換し、その上で回帰分析するようにします。 特に、質的変数が数字(数値ではない)で表現されているような場合は、そのままでも回帰分析できてしまうため、注意しなければなりません。

回帰分析の活用例

　最後に回帰分析の活用列をいくつか挙げておきます。

CVP分析(損益分岐点分析)：
CVP分析はビジネスで最も回帰分析が利用されるシーンの一つです。 CVP分析では、売上と経費の関係から、利益を上げるために必要な活動量(売上数など)を算出します。 ここで、売上額は単価×販売数で簡単に求まります。 しかし、経費は売上額のように簡単には求まりません。 なぜなら、売上額と違って経費は日々日頃から常に発生しているもので、その一つ一つを管理することはできないためです。 そこで過去の経費を記録し、記録した経費を回帰分析することで、活動量に対する経費を求めるようにします。

商品のコストパフォーマンスを算出：
回帰分析により商品のコストパフォーマンスを算出します。 売上は大きいがコストパフォーマンスの悪い商品は改善を検討すべきです。 また、コストパフォーマンスの悪い商品で、売上に貢献していない商品は廃止も検討すべきです。 ここで、コストパフォーマンスは粗利益率ではありません。 粗利益率はお店側が一方的に決められる値です。 対してコストパフォーマンスは、コストの割にどれだけ売れたかという、お客様が関与することによって定まる値です。

商品の売上傾向を調査：
未来予測できることが回帰分析の特徴の一つです。 よって、販売中の商品が今後どれくらい売れるか回帰分析することで予測できます。 特に新規に投入した新商品は、最初から売れることはそうそうなく、今後の売上が気になるところです。 投入後、それなりに時間が経過してから成長度を測った際に、成長が少ないようであれば改善を検討しなければいけません。 もしくは、その試みは失敗だったと早々に撤退する判断も必要です。 逆に、既存の商品でも売上の傾向を調査することがあります。 それは時期によって大きく売上が変動するような場合で、売れ始めとピークのタイミングを推し量るため、回帰分析します。