データ解析(手法)
その他の分析
- ・取り扱いはしておりませんが、その他、多変量解析に分類されている代表的な解析手法を紹介します。
- ・多変量解析できる統計ソフトとしては、無料のツールであればR、有料のツールであればSPSSが有名です。
- ・不明点あれば問い合わせください。
- ※当サイトで掲載しているデータは適当に作成したものであり、実際のものではありません。
判別分析
判別分析は、分析対象がどちらのグループに属するか判別する分析です。
判別は既知のデータ(何がどちらのグループに属しているか)に基づき行います。
データの例を以下に示します。
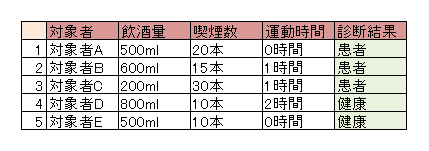
このようなデータから、例えば、「対象者F 飲酒400ml タバコ20本 運動1時間」が、健康グループか患者グループか、どちらに属するか判別できます。
よって、グループとそれに属する要素のデータがあらかじめ揃っていなければ分析できません。
および、1回の分析で判別できるグループは2つのみです。
グループ数が3つ以上ある場合は、再度、判別分析を繰り返すなどして分析しなければなりません。
というのも、分析対象に対して左右に分布があり、どちらの分布に近いかを判別することで分析しているためです。
この左右の分布がそれぞれ2つのグループに相当します。
このとき使う距離はマハラノビスの距離です。
そして基準となる線を引き、線より左側なら左側の分布、右側なら右側の分布、のように判別します。
この線を導出する関数を線形判別関数と言います。
となると当然、どちらの分布に近いか(どちらのグループに属するか)を明確に判別できない場合が発生します。
例えば、分布と分布の丁度中央に位置するような要素は判別が難しくなります。
このような場合は誤判別する可能性があり、誤判別の可能性も考慮した上で、判別分析していかなければなりません。
数量化2類
判別分析では、量的変数から成るデータを、どちらのグループに属するか判別していました。
これに対して、数量化2類では、質的変数から成るデータを、どちらのグループに属するか判別します。
データの例を以下に示します。
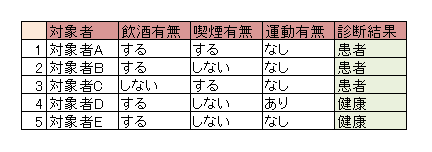
このようなデータから、例えば、「対象者F 飲酒する 喫煙する 運動なし」が、健康グループか患者グループか、どちらに属するか判別できます。
判別の仕方など、基本的な考え方は判別分析と同様です。
よって数量化2類は、判別分析を質的変数のデータに対応させた手法と言えます。
ロジスティック回帰分析
判別分析と似た手法にロジスティック回帰分析があります。 判別分析では、分析対象がどちらのグループに属するか判別していました。 対してロジスティック回帰分析では、分析対象が当該のグループに属する可能性を推定します。 つまり、判別分析ではAorBで分析していましたが、ロジスティック回帰分析ではA(もしくはB)となる確率を分析します。 よって、判別分析の分析結果は質的変数でしたが、ロジスティック回帰分析の分析結果は量的変数となります。 こうしたことから、例えば、開発した新商品が今後も売れ続けるかどうかの推定や、一過性の顧客かどうかを数値で分析することができます。
主成分分析
主成分分析は、サンプリングされたデータをより少ない軸で説明する分析です。
データの例を以下に示します。
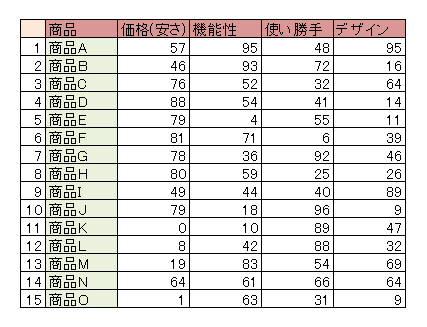
「より少ない軸で説明する」ということは、「その軸により多くの情報を含ませる」ということを意味します。
方針として、最も情報を含む方向に軸を設定することを考えます。
含まれている情報の量はバラつきに表れていることを踏まえると、最も分散の大きい方向に軸を設定すればいいということになります。
このように、主成分分析とは軸を導出する分析であり、軸を圧縮しているわけではありません。
また、軸の導出は分散で判断しており、データによって軸の設定の仕方が変わるということもありません。
主成分分析では、軸の導出は主成分分析によって行われるもので、アナリストがどのような軸としたいか決めるものではないのです。
2次元で捉えることが人間にとって最も理解しやすい形式であることから、主成分分析では軸は2つであることが一般的です。
そのため、さきほどの軸に対し直行する形で、分散が最大となる軸をもう一つ追加します。
もし軸のデータに対する説明力が不足している場合は、さらに軸を追加します。
しかし、あまり軸を増やしすぎると主成分分析の意味が薄まってしまうため、軸は通常2つ、多くても3つまでです。
そうして導出された軸を通してデータを眺めることで、より少ない軸でデータを説明できるようになります。
ただし、軸の意味までは主成分分析では分からないため、アナリストが意味を見出す必要があります。
数量化3類
主成分分析では、量的変数から成るデータに対して、軸を導出しました。
これに対して、数量化3類では、質的変数から成るデータに対して、軸を導出します。
データの例を以下に示します。
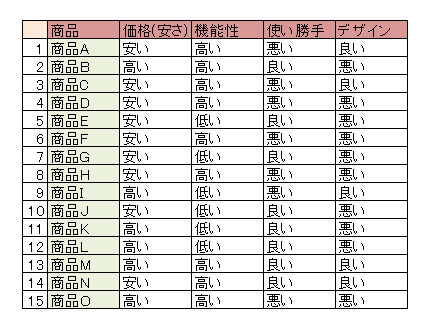
分析の仕方など、基本的な考え方は主成分分析と同様です。
よって数量化3類は、主成分分析を質的変数のデータに対応させた手法と言えます。
さらに、数量化3類と似た手法にコレスポンデンス分析があります。
それぞれ、手法が生み出された背景は異なるものの、類似の結果になることが知られています。
ただ、数量化3類が名義尺度を対象としていることに対して、コレスポンデンス分析は順序尺度も対象としています。
この点から、数量化3類よりもコレスポンデンス分析の方が対象範囲は広いようです。
因子分析
因子分析は、サンプリングされたデータの背景に、データを構成する因子があると考え、この因子を推定することで分析する手法です。 データの数より因子の数の方が少ないわけであり、つまり因子分析とは、より少ない因子でデータを説明する分析です。 これは、より少ない軸でデータを説明する主成分分析と似たような考え方です。 そして、因子分析と主成分分析はそれぞれ手段は異なりますが、同じような結果になることが知られています。 ゆえにどちらか一方を利用すればよく、一般的には主成分分析の方がよく利用されている傾向にあります。
多次元尺度構成法
多次元尺度構成法は、類似のデータ同士を近づけてマッピングすることでポジショニングマップを作成する分析です。 データ同士の類似度を評価し、その度合いを距離に置き換えてマッピングします(類似度が高ければ距離は近い)。 マッピングするにあたっては、先に空間の次元を決めておかなければなりません。 人間の特徴を考慮すると、2次元が最も理解しやすい形式であることから、次元は大抵の場合2(稀に3)となります。 「多次元尺度構成法」という名前でありながら、4次元以上の空間を定義することはまずありません。